题目:
题目概要:有一个n行m列的矩阵,每一个格子都有一个高度,路径只能从高处向低处扩散,问你如果最后一行可以全部被覆盖,最少要从第一行多少个格子开始,如果不能使最后一行全部被覆盖,求有多少个格子不能;
看完这道题,最直接的想法就是直接定义dx,dy两个数组表示上下左右走,看看第一行每一个格子能对应多少个最后一行的格子。
然后再设置一个vis数组表示最后一行是否已经被到达过,如果最后一行有点还没有被到达过,就输出0和vis=0的格子数量
但是当我们想要实现的时候,发现如果第一行的某个点对应的最后一行的点是断断续续的,那就很舒(e)服(xin)了
buuuut~

似乎可以证明,对于每一个第一行的点,他所对应的最后一行的点总是连续的
反证法:假设可以不连续
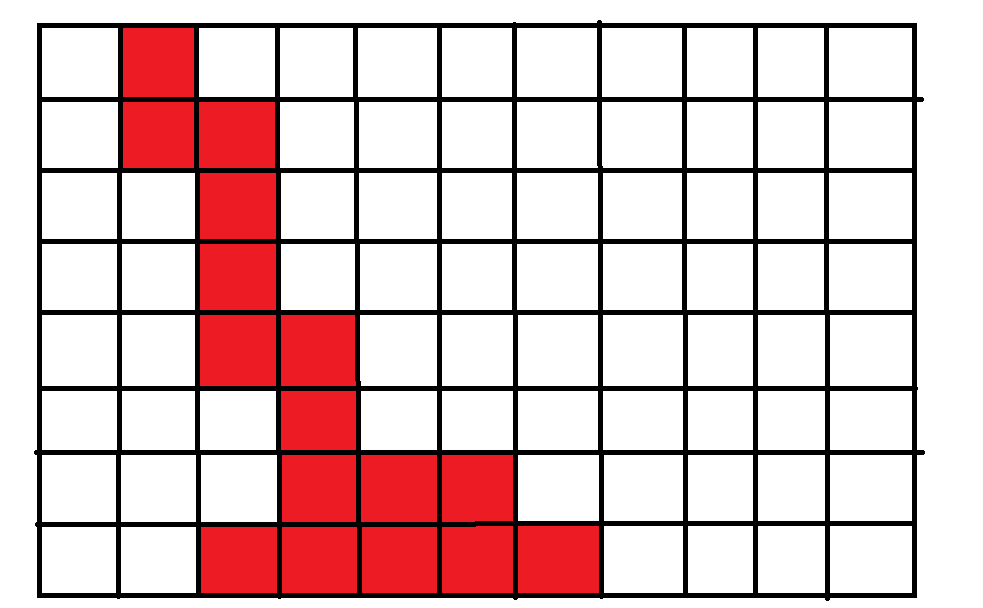
我们来看图
如图,这是一条从上到下的连续的路径,用红色标记
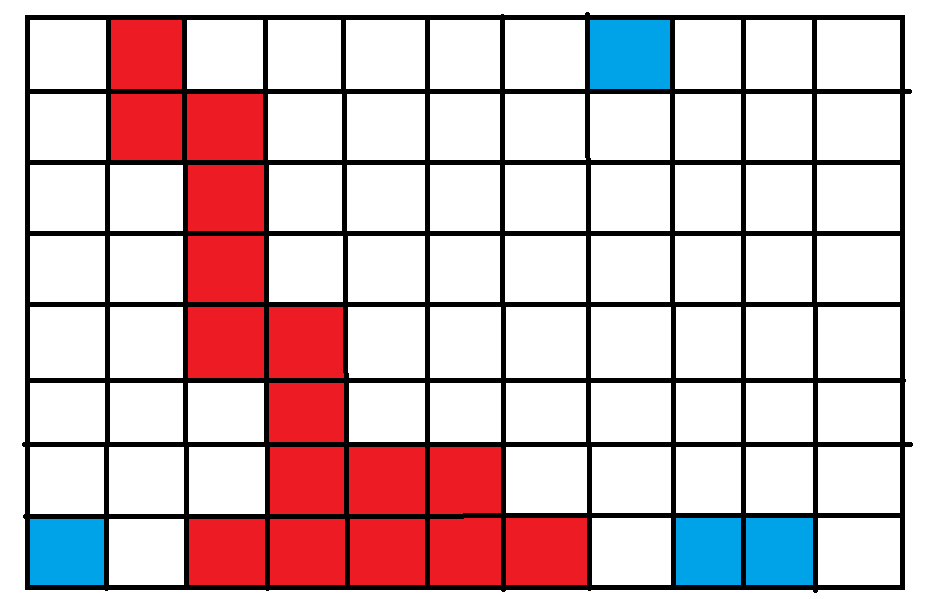
现在我们假设从第一行开始有这么一条路径不连续,如图,用蓝色表示
我们会发现,这样的话一定会有重合的路径,用紫色表示
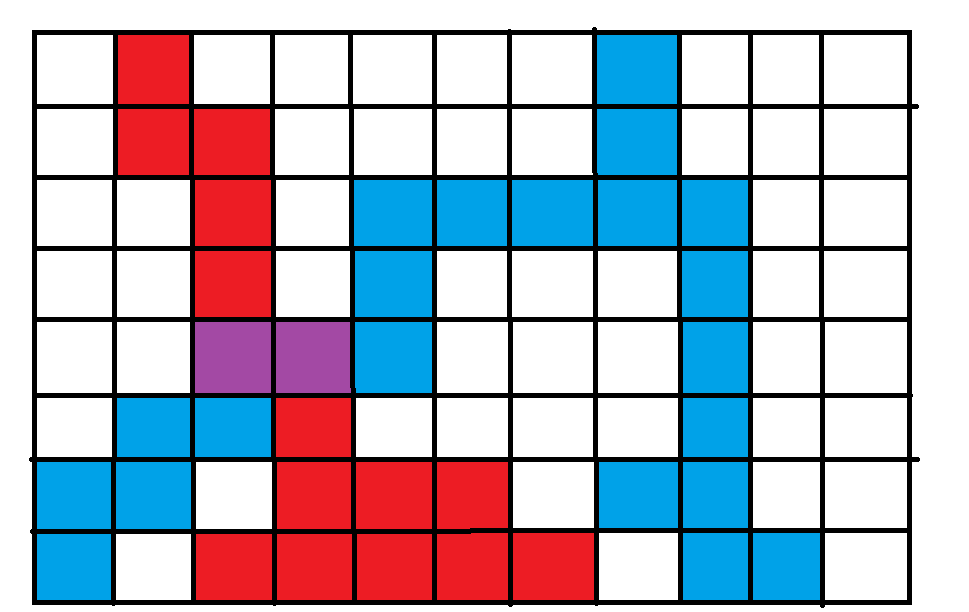
既然这样,从第一行蓝色点出发也一定能够到达最下层的红色点
那么最下面一行的区间一定是连续的,证毕(这里不连续是因为有无解的情况)
有了这个结论,只要不是无解的情况,把最后一行的连续区间拿出来,就变成了一个线段覆盖问题
代码:
1 #include2 #include 3 #include 4 #include 5 #include 6 #include 7 #include 8 #include 9 #include 10 using namespace std;11 typedef long long ll;12 ll read(){13 ll ans=0;14 char last=' ',ch=getchar();15 while(ch<'0' || ch>'9')last=ch,ch=getchar();16 while(ch>='0' && ch<='9')ans=ans*10+ch-'0',ch=getchar();17 if(last=='-')ans=-ans;18 return ans;19 }20 21 const int maxn=501;22 23 int n,m,atlas[maxn][maxn];24 int num[maxn][maxn];25 bool vis[maxn][maxn];26 int dx[4]={ 1,-1,0,0},dy[4]={ 0,0,1,-1};27 int l[maxn][maxn],r[maxn][maxn];28 29 //记忆化搜索 30 void dfs(int x,int y)31 {32 vis[x][y]=true;//先标记这个点到达过 33 for(int i=0;i<4;i++)//上下左右搜索 34 {35 int nx=x+dx[i],ny=y+dy[i];36 if(nx<1||nx>n||ny<1||ny>m) continue;//判断边界 37 if(atlas[nx][ny]>=atlas[x][y]) continue;//判断高度 38 if(!vis[nx][ny])dfs(nx,ny);39 l[x][y]=min(l[x][y],l[nx][ny]);40 r[x][y]=max(r[x][y],r[nx][ny]);//更新区间左右端点 41 }42 }43 44 int main()45 {46 n=read(),m=read();47 memset(vis,false,sizeof(vis));48 memset(l,0x3f,sizeof(l));//初始化 49 for(int i=1;i<=m;i++)50 {51 l[n][i]=r[n][i]=i;//区间初始化 52 }53 for(int i=1;i<=n;i++)54 {55 for(int j=1;j<=m;j++)56 {57 atlas[i][j]=read();58 }59 }60 61 for(int i=1;i<=m;i++)62 {63 if(!vis[1][i]) dfs(1,i);//如果还没有被到达过,就搜索 64 }65 66 int counti=0;67 for(int i=1;i<=m;i++)68 {69 if(!vis[n][i]) counti++;70 }//看最后一行有没有不能到达的 71 if(counti!=0) 72 {73 cout<<0< <